Solving equations with variables on both sides is a fundamental algebra skill, essential for more advanced math concepts. These equations require strategic steps to isolate the variable, ensuring accuracy and understanding. Worksheets and online resources provide ample practice opportunities, helping students master this critical skill for real-world problem-solving.
Definition and Importance
Solving equations with variables on both sides involves algebraic expressions where the variable appears on both sides of the equal sign. This type of equation requires strategic manipulation to isolate the variable, ensuring the solution is accurate. Mastering this skill is crucial for advancing in algebra, as it forms the foundation for more complex problem-solving. Worksheets and online resources provide structured practice, helping students understand the principles and apply them effectively. The ability to solve such equations is essential for real-world applications, making it a cornerstone of mathematical literacy and problem-solving expertise.
Key Objectives for Solving Such Equations
The primary objectives when solving equations with variables on both sides include mastering the ability to simplify complex expressions, strategically applying inverse operations, and ensuring the equation remains balanced throughout the process. A key goal is to isolate the variable efficiently while avoiding common errors like improper distribution or misapplying operation order. Additionally, students aim to develop problem-solving strategies that enhance algebraic thinking and logical reasoning. By achieving these objectives, learners build a solid foundation for tackling more advanced mathematical concepts and real-world problems that require precise equation manipulation and critical analysis.
Common Challenges and Mistakes
When solving equations with variables on both sides, students often face challenges such as incorrectly applying inverse operations or failing to maintain balance by performing the same operation on both sides; A common mistake is mishandling negative signs or misapplying the distributive property, which can lead to incorrect solutions. Additionally, learners may struggle with combining like terms effectively or moving variables to the same side without reversing the inequality sign when necessary. Overlooking these steps can result in inaccurate solutions and a poor understanding of algebraic principles. Recognizing these mistakes early on helps learners develop better problem-solving habits and improve their overall proficiency in equation solving.

Steps to Solve Equations with Variables on Both Sides
Solving equations with variables on both sides involves simplifying both sides, applying inverse operations to isolate the variable, and verifying the solution’s accuracy.
Simplifying Both Sides of the Equation
Simplifying both sides of the equation is the first step in solving equations with variables on both sides. This involves removing parentheses, combining like terms, and ensuring the equation remains balanced. Start by distributing multiplication over addition or subtraction on both sides. Next, combine like terms by adding or subtracting coefficients of the same variable. For example, in the equation (2x + 3 = x + 5), simplify by subtracting (x) from both sides to get (x + 3 = 5). Always check each term after simplifying to ensure no errors were made. This step sets the foundation for isolating the variable and finding the solution.
Using Inverse Operations to Isolate the Variable
After simplifying both sides, the next step is to use inverse operations to isolate the variable. Inverse operations are pairs of operations that undo each other, such as addition and subtraction or multiplication and division. For example, if you have 2x + 3 = 5, subtract 3 from both sides to get 2x = 2. Then, divide both sides by 2 to isolate x, resulting in x = 1. Always apply the same operation to both sides to maintain the equation’s balance. This method ensures the variable is isolated on one side, allowing you to find its value accurately. Regular practice helps master this critical skill in algebra.
Checking the Solution for Accuracy
After isolating the variable, it’s crucial to verify the solution by substituting it back into the original equation. This ensures that both sides of the equation are equal, confirming the solution’s accuracy. For example, if you solve for x and find x = 4, replace x in the original equation with 4 and simplify both sides. If both sides yield the same result, the solution is correct. This step helps catch any calculation errors made during the solving process; Regularly checking solutions builds confidence and reinforces the understanding of equation-solving principles. Always make this verification a habit to ensure reliable results in every problem.

General Strategies for Solving Linear Equations
When solving linear equations, focus on isolating the variable by performing the same operation on both sides. Simplify expressions by combining like terms and eliminating variables from one side. Always check your solution by substituting it back into the original equation to ensure equality. Consistency and attention to detail are key to avoiding errors and achieving accurate results.
Getting Variables on the Same Side
To solve equations with variables on both sides, aim to move all variable terms to one side and constants to the other. This can be achieved by adding, subtracting, or multiplying both sides of the equation to maintain balance. For example, if the equation is 2x + 3 = 4x, 2, subtract 2x from both sides to get 3 = 2x — 2. This simplifies the equation by consolidating variables on one side. Always apply the same operation to both sides to ensure equality is preserved. This strategy helps in isolating the variable effectively and reduces complexity.
Combining Like Terms Effectively

Combining like terms is a critical step in solving equations with variables on both sides; Like terms are terms that have the same variable raised to the same power. For example, in the equation 3x + 2 + 4x ⎼ 5 = 7, combine 3x and 4x to get 7x, and 2 and -5 to get -3. This simplifies the equation to 7x ⎼ 3 = 7. Always look for opportunities to combine like terms on both sides of the equation to make it easier to isolate the variable. This step ensures the equation remains balanced and simplifies the path to finding the solution.
Applying the Same Operation to Both Sides
When solving equations with variables on both sides, applying the same operation to both sides is essential to maintain balance. For instance, if you add or subtract a number from one side, you must do the same to the other. This ensures equality is preserved. For example, in the equation 2x + 5 = 3x — 2, subtracting 2x from both sides gives 5 = x ⎼ 2. Then, adding 2 to both sides yields x = 7. This method helps isolate the variable and find its value. Always perform operations evenly on both sides to avoid disrupting the equation’s balance.

Examples of Solving Equations with Variables on Both Sides
Examples simplify learning by providing practical demonstrations. Numerical and word problems illustrate step-by-step solutions, helping users master equations with variables on both sides effectively.
Numerical Examples
Numerical examples are essential for understanding how to solve equations with variables on both sides. For instance, consider the equation 2x + 3 = x + 5. To solve, subtract x from both sides, resulting in x + 3 = 5. Then, subtract 3 from both sides to find x = 2. Another example is 4y ⎼ 2 = 3y + 6. Subtract 3y from both sides to get y ⎼ 2 = 6, then add 2 to both sides, yielding y = 8. These step-by-step solutions demonstrate how to isolate variables effectively. Practicing numerical examples helps build problem-solving skills and algebraic intuition.
Word Problem Examples
Word problems involving equations with variables on both sides often reflect real-life scenarios. For example, imagine Sarah and Emily are saving money for a trip. If Sarah has saved $12 more than twice what Emily has, and Emily has saved $5 more than Sarah, the equation 2E + 12 = S and S = E + 5 can be used. Solving these, substitute S in the first equation: 2E + 12 = E + 5. Subtract E from both sides: E + 12 = 5, then E = -7, which may indicate an error in the problem setup. Another example: A car travels 15 mph faster than a bike, and their speeds add up to 35 mph. Setting up the equation B + (B + 15) = 35, solve to find B = 10 mph and the car’s speed is 25 mph. These examples highlight how to translate verbal descriptions into solvable equations. Practicing word problems enhances critical thinking and algebraic application.
Case Studies and Real-World Applications
Educators often use real-world scenarios to teach solving equations with variables on both sides. For instance, budget planning involves balancing income and expenses. Suppose a company’s revenue equals its expenses plus profit: R = E + P. If revenue is also calculated as R = 2E + 150, solving these equations reveals how expenses and profits relate. Another example is engineering, where forces in equilibrium are modeled by equations like F1 + F2 = F3 + F4. Such case studies help students apply algebraic principles to practical problems, fostering problem-solving skills and critical thinking. These applications bridge the gap between abstract math and everyday situations, making learning more meaningful and relevant.

Practice Exercises and Worksheets
Engage with targeted worksheets to master solving equations with variables on both sides. These resources offer structured exercises, from basic to advanced levels, ensuring comprehensive skill development.
Worksheets for Beginners
Beginner-friendly worksheets are designed to introduce students to solving equations with variables on both sides. They feature step-by-step examples, simple problems, and clear instructions to build foundational skills. These worksheets typically start with basic equations and gradually introduce more complex scenarios, ensuring a smooth learning curve. Many resources include visual aids, such as number lines or algebra tiles, to help visualize the problem-solving process. Worksheets are often downloadable as PDFs, making them easy to access and print. They also include answer keys, allowing students to self-check their work and understand their mistakes. Interactive versions may include fillable fields for digital completion, catering to modern learning preferences.
Advanced Practice Problems
Advanced practice problems are designed for students who have mastered the basics of solving equations with variables on both sides. These problems introduce more complexity, such as multi-step equations, nested variables, and real-world applications. They often require students to apply critical thinking and problem-solving strategies. Worksheets for advanced learners include challenging scenarios, such as equations with fractions, decimals, or multiple variables. These exercises help strengthen algebraic manipulation skills and prepare students for higher-level mathematics. Many resources offer PDF worksheets with detailed solutions, enabling students to track their progress and identify areas for improvement. Advanced problems also encourage the development of analytical reasoning and mathematical fluency, essential for tackling more complex equations in the future.
Interactive Quizzes and Online Resources
Interactive quizzes and online resources provide an engaging way to practice solving equations with variables on both sides. Websites like Khan Academy, Quizlet, and Mathway offer interactive exercises that test understanding and provide immediate feedback; Many platforms include step-by-step solutions, video tutorials, and adaptive learning tools to cater to different skill levels. Some resources allow users to create custom quizzes or track progress over time. Additionally, online worksheets with interactive elements, such as fill-in-the-blank questions or multiple-choice problems, make learning more dynamic. These tools are particularly helpful for reinforcing concepts and identifying areas that need more practice, ensuring a comprehensive understanding of equation-solving skills.
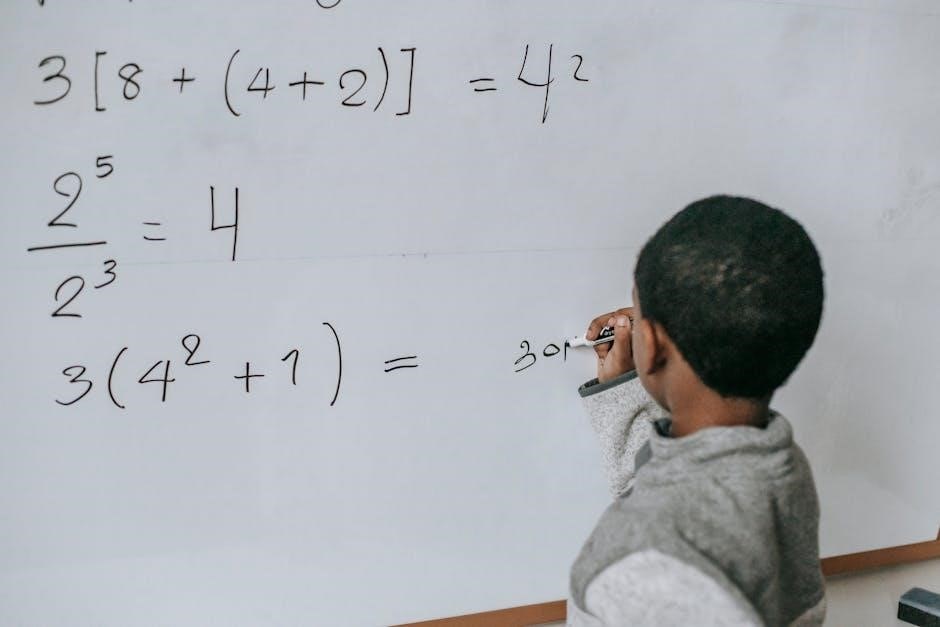
Resources for Learning and Teaching
Explore educational websites offering free PDF worksheets and teaching guides for solving equations with variables on both sides, perfect for classroom or self-study use.
Recommended Websites and Tools
For effective learning and teaching, numerous websites provide excellent resources for solving equations with variables on both sides. Khan Academy offers free step-by-step guides and practice exercises, while Mathway provides an interactive equation solver. IXL features adaptive worksheets and real-time feedback, making it ideal for both students and teachers. CK-12 offers customizable worksheets and interactive simulations. Additionally, Teachers Pay Teachers has a wide range of downloadable PDF worksheets specifically designed for this topic. These tools cater to diverse learning styles and skill levels, ensuring comprehensive understanding and mastery of solving equations with variables on both sides.
PDF Worksheets and Answer Keys
High-quality PDF worksheets and answer keys are essential for practicing and mastering equations with variables on both sides. Websites like Teachers Pay Teachers and Worksheet Genius offer a variety of downloadable resources tailored to different skill levels. These worksheets often include step-by-step instructions and examples, making them ideal for self-study or classroom use. Many PDFs are free or low-cost, with answer keys provided to help students and educators assess progress. They cover topics like simplifying equations, combining like terms, and applying inverse operations. These resources are perfect for reinforcing concepts and ensuring a strong foundation in solving equations with variables on both sides.

Video Tutorials and Guides
Video tutorials and guides are excellent resources for understanding how to solve equations with variables on both sides. Platforms like YouTube and Khan Academy offer free, high-quality tutorials that break down complex concepts into easy-to-follow steps. Channels such as 3Blue1Brown and Math Antics provide engaging animations and real-world examples to enhance learning. These videos often include voiceover explanations, step-by-step solutions, and tips for avoiding common mistakes. They cater to different learning styles, making them ideal for visual and auditory learners. Additionally, many educational websites embed video guides directly into their worksheets, allowing students to learn and practice simultaneously. These resources are invaluable for students seeking additional support or clarification.
Assessment and Feedback
Quizzes, assignments, and projects evaluate understanding. Peer review fosters collaboration and identifies areas for improvement. Immediate feedback helps students refine their problem-solving skills effectively.
Grading Criteria for Assignments
Assignments are graded based on accuracy, problem setup, and algebraic manipulation. Points are awarded for correctly simplifying equations, isolating variables, and applying inverse operations. Neatness and logical presentation are also evaluated. Partial credit is given for correct steps, even if the final answer is incorrect. Instructors assess understanding of key concepts, such as combining like terms and maintaining balance in equations. Feedback highlights strengths, areas for improvement, and common errors. Detailed rubrics ensure transparency and consistency in grading. Students are encouraged to review feedback to refine their skills and approach to solving equations with variables on both sides effectively.

Common Errors and How to Avoid Them
Common mistakes include incorrectly handling negative signs, misapplying the distributive property, and forgetting to apply operations to both sides of the equation. Students often struggle with combining like terms and may accidentally drop variables or constants. To avoid these errors, carefully check each step and ensure operations are applied consistently. Simplify both sides of the equation before attempting to solve for the variable. Use reversal techniques to isolate the variable, and verify solutions by substituting them back into the original equation. Practicing step-by-step methods and reviewing examples can help build confidence and reduce mistakes.
Peer Review and Collaboration
Peer review and collaboration are essential for improving problem-solving skills when working on equations with variables on both sides. Students can exchange worksheets and review each other’s solutions, identifying errors and suggesting corrections. This process fosters a deeper understanding of the material and encourages critical thinking. Collaborative learning allows students to discuss different approaches, reinforcing their grasp of equation-solving techniques. Encourage learners to explain their reasoning, as articulating solutions can clarify their own understanding. Additionally, peer feedback helps build confidence and teamwork skills, making the learning process more engaging and effective. Regular collaboration enhances problem-solving accuracy and speeds up mastery of complex equations.
